Evolving our understanding – genetic algorithms explained: Part 4

In my last blog, we explored how genetic algorithms can assist scheduling engineers to improve their schedules, over a traditional manual approach of using a spreadsheet solution to generate mining sequences. So now that we have an understanding of how genetic algorithms and spreadsheets can be used in the scheduling space, what other solutions exist?
Before we evaluate current technologies, let’s take a short history lesson to understand where we have come from. Mathematician K.F. Lane was crucial to life-of-mine schedule optimisation, as he was among the first to discuss the topic in his book Choosing the Optimum Cutoff Grade back in 1964. The Lerchs-Grossman algorithm, published in Optimum Design of Open-Pit Mines by Helmut Lerchs and Ingo Grossman in 1965, is still used today.
Limitations at the time meant mathematicians were not able to apply their theories to real-world problems to be solved in a reasonable time. Since then, advancements in technology allows us to throw massive processing power at these problems. For almost 40 years, the mining industry has been talking about commercial programs that can help solve mine scheduling problems.
So, how hard can it be? The problem of scheduling a mine site is classified as NP-Hard. This term indicates that the problem is not only complex, but also difficult to evaluate all options available. Evaluating all the possible options to come up with the optimum solution would take an incredible amount of time, even with all the computer power available to us today.
Consider the real-world requirements of constraints such as cutoff grade, pit size, per-period mill or blend targets, spatial constraints and the non-linear interaction between them all—the problem cannot be easily solved using classical techniques without a level of simplification.
Linear programming (LP) can be used to achieve the best outcome for a model whose requirements are represented by a linear relationship. In mine sequencing scenarios, not all relationships can be represented linearly, therefore, to solve such a scenario requires simplification until it only has linear relationships.
An LP model is a simplified representation of a mine site with a set of variables and linear inequalities, e.g. a variable could be created representing the proportion of material taken from block X in period P and sent to destination M. This variable could be used in constraints such as:
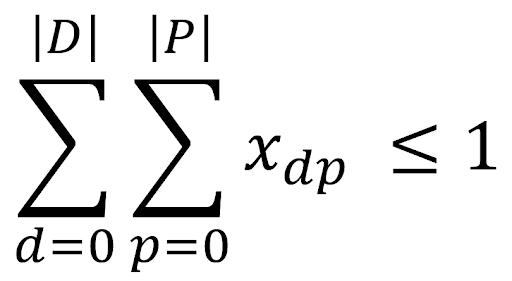
The proportion of material in block X that was sent to all destinations over all periods can’t be greater than 1. We also can’t include any non-linear considerations, such as digging rates being affected by nearby equipment or complicated plant processes.
In addition, LP solutions struggle to solve mine scheduling problems due to their sheer scale. A simple model with 6 pushbacks, 12 benches and 10 periods would lead to 1.9×1033 possible extraction sequences. To get around this, we must simplify the model, e.g. use larger blocks, break down by less periods, or include less destinations.
Linear programming focuses on manipulating a single solution, in contrast to a genetic algorithm, which exploits multiple solutions.
Genetic algorithms were introduced to reduce the simplification, relying on their ability to use complex evaluation functions. Genetic algorithms are a considerably faster mechanism for determining a result; however, those results are typically classified as ‘near optimal’. The inherent nature of LP means their runtime is long, but they are guaranteed to find the optimal solution.
In this example, an LP and a GA are given the same problem: find the largest size circle to fit into a constrained area. You’ll note that the LP traverses the entire search space, but the GA combines the best of multiple solutions to quickly come to a near optimal result.
Using GA vs LP is a trade off. Using LP you risk over-simplifying the data to fit into a suitable model, with the result considered as optimal. With GA, much less simplification is necessary and run time is short in comparison to LP, with results considered near-optimal.
For the last five years, Maptek Evolution has relied on genetic algorithms to optimise schedules using large models in a reasonable amount of time. This enables users to maximise the value of deposits without compromising operations or over-simplification.
< Click here to read part 3 of this blog series