Evolving our understanding – genetic algorithms explained: Part 2

In our previous blog, we covered the basics of evolutionary algorithms—how they work and how we use them at Maptek. In Part 2 we explain how we work with advances in evolutionary computing theory.

Traditionally, the most important thing for a good genetic algorithm was a good genome combined with good genetic operators. 

A genome is a minimal representation of a particular solution to a given problem, and genetic operators are ways to manipulate these genomes in order to create new individuals. As in nature, a good genetic algorithm should not destroy previous progress in the name of new exploration. It should also not stifle new exploration in order to maintain previous progress. 

So how do we manage these conflicting aims, which typically require highly specific genomes and crossover operators to best address a given problem? The result is often many similar, yet distinct implementations of genetic algorithms with minimal-to-no shared code.

One of the main benefits of genetic algorithms is the ability to compare tradeoffs between competing objectives. This is achieved by the algorithm returning multiple potential solutions, allowing the user to decide between them.

Genetic algorithms provide a unique approach to optimising multiple competing objectives. For example, if you were planning a cross country trip in your car, you may want to minimise distance, or you may want to maximise the number of attractions that you see. There is a negative correlation between these two objectives—the more attractions you see, the further you have to drive. Genetic algorithms provide the ability to target both of these objectives at once, and offer several potential tradeoffs to pick from.

The Maptek scheduling program Evolution uses a genetic algorithm approach called Non-dominated Sorting Genetic Algorithm (NSGA-II). The NSGA refers to the method that is used to determine if one individual in the population is fitter than another. 

Consider the example above. If we only cared about a single objective—minimising distance—determining if one individual is fitter than another is simple. We would check the total distance travelled when following the route described in individual solutions A and B. If the distance is shorter in A, then A is fitter than B. 

Now consider the situation where we care about both total distance and attractions visited. In this case, Individual A with a shorter distance is fitter in our distance objective, but Individual B could visit more attractions, making it fitter in our attraction objective.

In scenarios with multiple objectives, there will typically be tradeoffs between them. Depending on the criteria, some results may appear better for certain problems, but each solution will technically be equally as good. 

As above, if Individual A had both a shorter distance and visited more attractions, then Individual A is fitter than B in all objectives. In the context of NSGA, this relationship is described as Individual A dominates Individual B. If Individual A has no other individuals that dominate it, it is known as non-dominated. The result of the NSGA algorithm is a set of non-dominated individuals, all with different trade-offs between objectives.

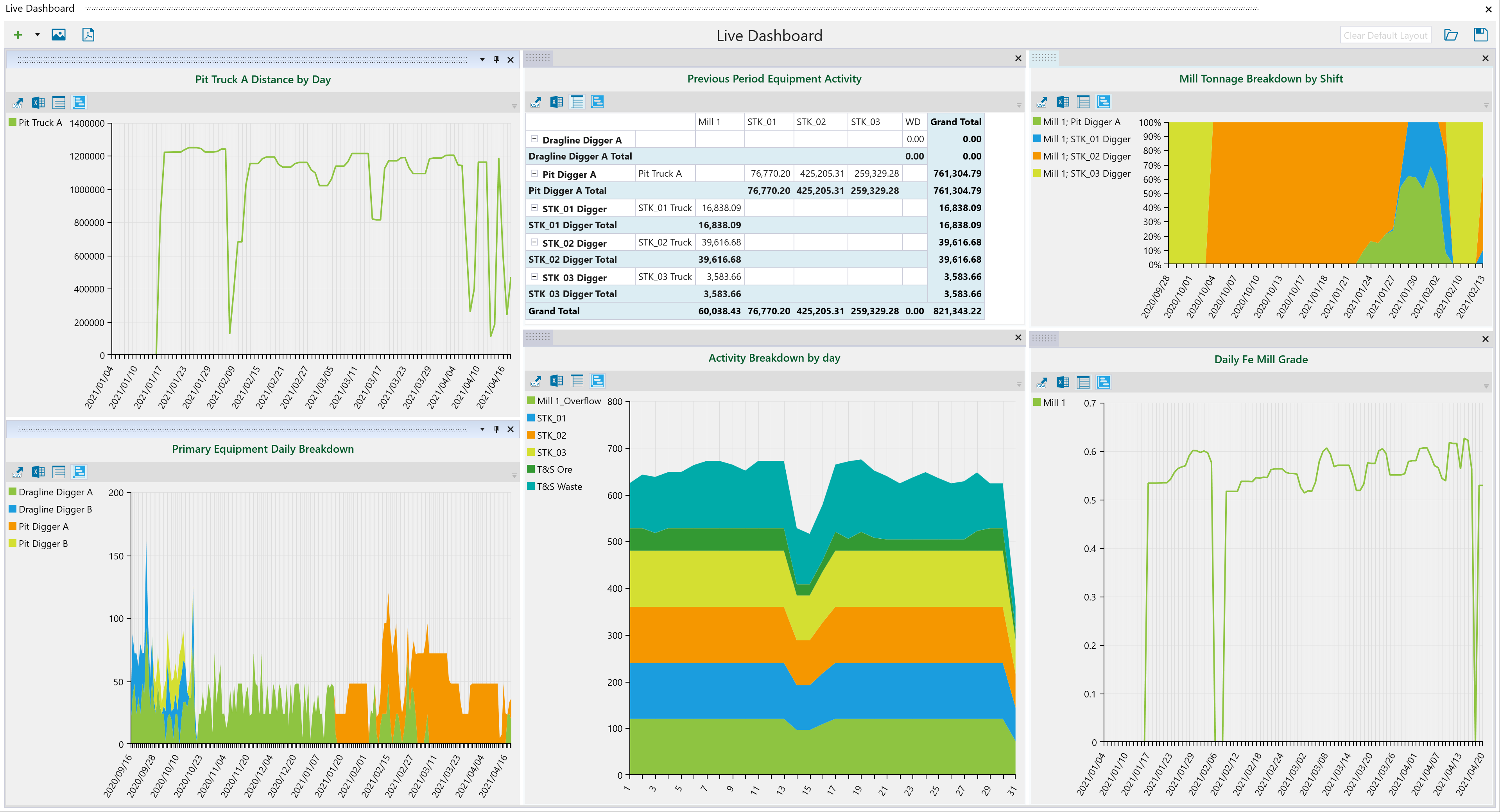
Dashboards help schedulers refine equipment utilisation for an existing sequence, using pivots to focus on meeting mill targets.

The number of objectives that can be handled with traditional genetic algorithms is quite small, with the commonly used NSGA-II recommending three or less. A large number of objectives causes most individuals to be non-dominated in at least one objective. Additionally, the methods for judging algorithm completeness and selection are heavily correlated to the number of objectives. This means that as the number of objectives rise, so does the proportion of program run time that is spent working on these methods.

Genetic algorithm improvements have allowed newer iterations to handle ‘many-objective’ problems. In 2013, an improved algorithm, NSGA-III was proposed, increasing the number of objectives that could be handled to about 15. This approach can produce strong results with no significant performance degradation.

The improvements brought by NSGA-III are problem invariant, meaning all genetic algorithms that are ‘many-objective’ will see an improvement when upgrading to NSGA-III. This is why we have embarked on intelligently consolidating functionality between the multiple genetic algorithms for Maptek software engineers to use. 

This consolidation must allow for complete customisation of genomes and genetic operators to ensure that we keep the historical benefits of highly targeted optimisation. It must also allow access to advanced, multi-objective genetic problem-solving functionality so that customers can realise the substantial benefits through the solutions we provide.

With programming, it’s survival of the fittest!

Click here to read part 3 of this blog series >

< Click here to read part 1 of this blog series